Rayleigh’s monotonicity principle and AM-GM-HM inequalities |

Rayleigh’s monotonicity principle states that if the resistances of a circuit of resistors are increased, the effective resistance between any two points can only increase. If they are decreased, they can only decrease. You can find a short proof in the Doyle-Snell book right here.

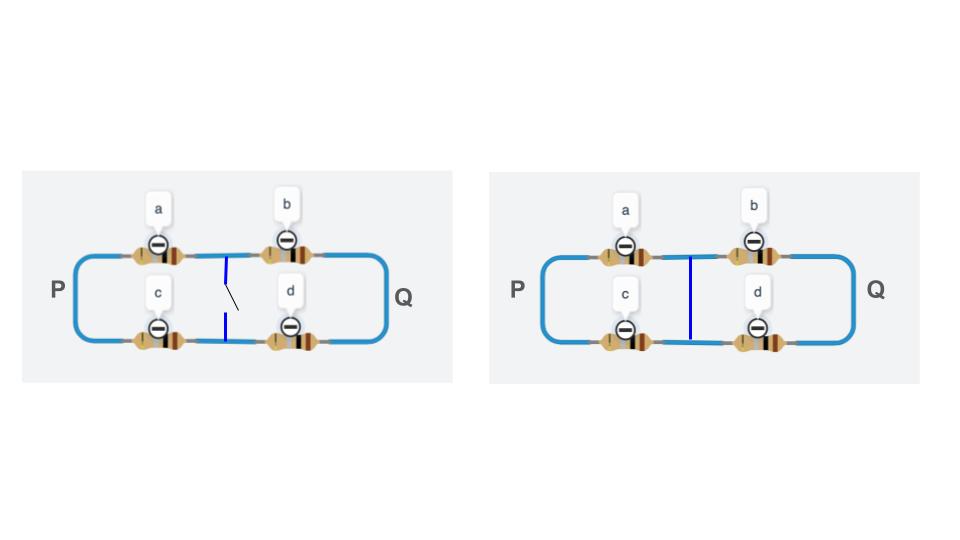
One can use this intuitive principle to prove classic and other non-trivial inequalities. Here is the solution to exercise 1.4.2 from the Doyle-Snell book. In the figure below, we have two circuits of resistors (say of resistances $a, b, c, d$ ).The difference between the left and the right one, is that we close a switch and thus we change the resistance between the corresponding points from $+\infty$ to 0. This is also called short-circuiting. By Rayleigh’s monotonicity principle, the effective resistance between P,Q of the left circuit is larger than the corresponding effective resistance of the right circuit. By using the standard in-series and in-parallel equivalent resistors, we obtain that the effective resistance between P,Q for the left circuit is $R=\frac{1}{\frac{1}{a+b}+\frac{1}{c+d}}$ while for the right one $R' = \frac{1}{\frac{1}{a}+\frac{1}{c}}+\frac{1}{\frac{1}{b}+\frac{1}{d}}$ . 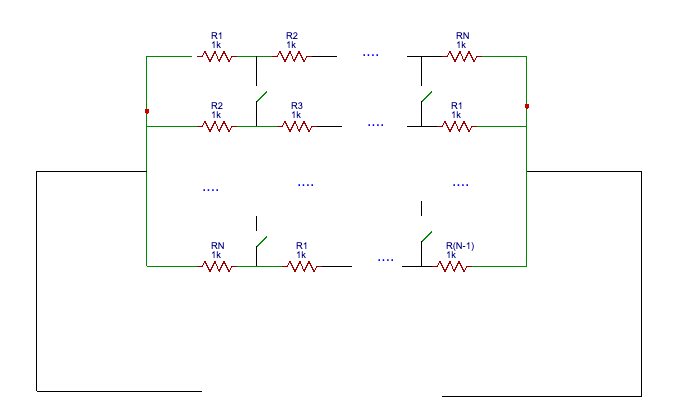Combining the above gives the following inequality: $\frac{1}{\frac{1}{a+b}+\frac{1}{c+d}} \geq \frac{1}{\frac{1}{a}+\frac{1}{c}}+\frac{1}{\frac{1}{b}+\frac{1}{d}}$ .

Let’s consider the following special case: $c=b, d=a$ . We obtain the arithmetic-harmonic mean for two terms inequality $\frac{1}{\frac{1}{a+b}+\frac{1}{c+d}}=\frac{a+b}{2}\geq \frac{2ab}{a+b}$ . We can obtain the general inequality $\frac{1}{n} \sum_{i=1}^n R_i \geq \frac{n}{\sum_{i=1}^n \frac{1}{R_i}}$ . by the applying Rayleigh’s monotonicity principle between the following circuit and the one obtained where we close all switches.